Stellar Radiation & Stellar Types
Nuclear Fusion
A star forms out of a slowly condensing cloud of gas. As the pressure and density in the core increase so does the temperature. At a certain point a critical temperature is reached at which nuclear fusion can occur. Nuclear fusion is the process of combining nuclei to make a nucleus with a greater number of protons and neutrons.
Deep inside the Sun the temperature reaches 15 million K. At such an extreme temperature the positively charged atomic nuclei are moving at high speed. Occasionally two charged particles will collide with sufficient energy so that they stick together. This is the fundamental process that occurs in all stars.
Proton-Proton Chain
The simplest reaction to be found in stars is the conversion of hydrogen into helium - a process known as the proton-proton chain. In this process six hydrogen atoms are needed to create one helium nucleus of two protons and two neutrons.
|
Process |
Result |
Extras |
|
| 1 | proton + proton | deuterium | positron, neutrino |
| 2 | proton + deuterium | helium-3 | gamma-ray |
| 3 | helium-3 + helium-3 | helium-4 | 2 protons |
In Step 1 two protons come together to form deuterium (a nucleus of one proton and one neutron). This interaction also involves the liberation of a positron (a positively charged electron) and a neutrino. This process occurs 1038 times per second in the Sun.
In Step 2 the resulting deuterium nucleus combines with a proton to make the rare isotope helium-3 consisiting of one neutron and two protons. This reaction also produces a gamma-ray.
In Step 3 the helium-3 nucleus becomes a helium-4 nucleus by the addition of a neutron. This step can occur in several ways, but the combination of two helium-3 nuclei is the most common way.
Steps 1 and 2 must occur twice before step 3 can occur. Six protons go into the cycle, but two come back out. The overall process results in 4 protons (hydrogen nuclei) becoming a helium-4 nucleus, two positrons, two neutrinos and two gamma-rays.
Each helium-4 nucleus has a mass that is about 99.3% of the mass of four protons. In the Sun, for example, 600 million tons of hydrogen are converted into 596 million tons of helium every second. The missing four million tons of matter is released as energy in accordance with Einstein's equation E=mc2.
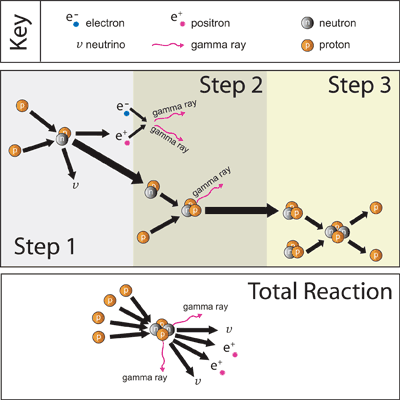 |
|
Figure 2.1: Proton-Proton Chain |
CNO Cycle
The other major process that occurs in more massive stars (due to the necessary higher core temperature) is the Carbon-Nitrogen-Oxygen (CNO) cycle. This more complex process involves the combination of carbon-12 nuclei with protons to form successively heavier nuclei up to oxygen. More details on the CNO cycle can be found in booklet 5 - 'Stellar Processes and Evolution' under the chapter of Nucleosynthesis.
Hydrostatic Equilibrium
When a star forms, gravity is the dominant force causing a cloud of interstellar gas to condense. As nuclear fusion begins the outward radiation, pressure resists the inward pull of gravity and halts any further contraction. The star is now in equilibrium: the energy generated by nuclear fusion in the stellar core radiates outwards, balancing the force of gravity pulling the star inward.
This balance is called Hydrostatic Equilibrium (or sometimes gravitational equilibrium). At any point within a star in hydrostatic equilibrium the underlying pressure supports the weight from the overlying material. The equation for hydrostatic equilibrium is shown below.
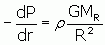 |
The Sun is currently in this stable state and will remain so for another 5000 million years. At this point all the fuel in the Sun will have been used up and, since it is no longer able to generate an outward radiation pressure, gravitational contraction will begin again.
Luminosity & Apparent Brightness
The luminosity (L) is the energy radiated into space per unit time. This energy takes several forms, but the majority is released as electromagnetic radiation. The Sun has a luminosity of 3.8 x 1026 Watts. By comparison in 2002 there were 441 commercial nuclear reactors in the world producing 358 x 109 Watts. They would have to run at full power for 50 million years to produce the same output as the Sun in one second!
Apparent Brightness
A star's apparent brightness is described as the amount of energy that actually reaches us per unit area of the star. Apparent brightness is also referred to as flux. The diminishing of apparent brightness obeys the inverse square law. If the radiation from a star is emitted uniformly in all directions (spherically), then doubling the distance from the star means the radiation intensity per unit area falls by one quarter.
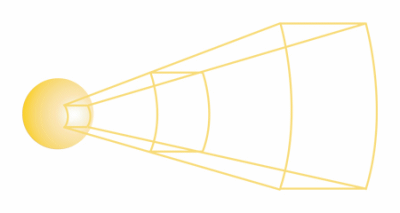 |
|
Figure 2.2: Square Law for Areas |
Apparent brightness, which is measured in units of watts per square metre, can be calculated using the following equation:
 |
Astronomers measure apparent brightness using an electronic detection device, such as a CCD, which records how much energy strikes its surface each second.
Blackbody Radiaton
Astronomers consider stars to be an example of a blackbody - the term given to a perfect radiator and absorber of energy, with no reflecting power. This perfection refers to the absorption of all the electromagnetic energy, or radiation, that strikes it each second. Blackbody radiation is the radiation emitted from a body that is in a thermo-dynamic equilibrium. The concept of a blackbody is a theoretical one (a perfect absorber and radiator is thought not to exist in reality) but deep inside, a star is probably as close to these conditions as anywhere else. This means that we can use the theory for blackbody radiators to infer details about stars.
Blackbody radiation was first studied by the German physicist Max Planck, who came up with the equation that gives the energy emitted per second from 1 cm2 of a blackbody's surface. The equation, called Planck's radiation law is written as follows:
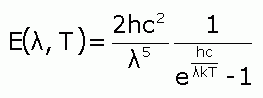 |
Plotting the results for a range of temperatures as a function of wavelength produces a characteristic radiation curve.
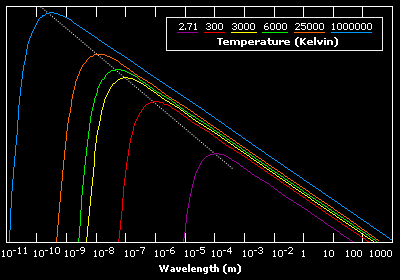 |
Figure 2.3: Variance in Blackbody Curves with Temperature
The shape of each curve is the same. The only difference is that with higher temperatures the peak radiation intensity is higher. The peak intensities at each temperature are related as defined by Wien's Law.
Wien's Law
While our eyes only see a very small part of the electromagnetic spectrum, objects can absorb and emit light at wavelengths we cannot see. A hotter object will produce more radiation, but the wavelength is shifted from the red end of the spectrum to the blue.
Astronomers are able to calculate a star's temperature by working out the wavelength at which it emits its maximum light. Wien's (displacement) Law relates the temperature of an object to the maximum wavelength at which it radiates energy, since as the temperature of an object increases the maximum wavelength will decrease. In this way, stars of different temperatures appear as different colours in the electromagnetic spectrum, with hotter stars appearing bluer and cooler stars appearing redder.
Wien's Law is written as follows:
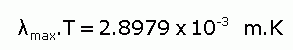 |
Stefan-Boltzmann Law
The Stefan-Boltzmann law tells us how much energy a blackbody radiator of a known temperature radiates per unit area of its surface. It states that the radiated electromagnetic energy of a hot body is proportional to the surface area radiating that power, and the fourth power of the thermodynamic temperature. It can be used to calculate the total energy emitted per square centimetre in all directions.
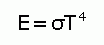 |
Stellar Spectra
Objects of different temperatures emit spectra that peak at different wavelengths (as indicated by Wien's Law) so that hotter objects emit most of their radiation at shorter wavelengths, appearing bluer, while cooler objects emit most of their radiation at longer wavelengths, therefore appearing redder.
Scientists use a spectrograph to split the spectrum of the star they are studying. Examining spectra allows astronomers to find out what stars are made of, their structures and their past.
When looking at light that has travelled through the atmosphere of a star, (effectively a low density gas) scientists observe black lines in the spectrum, known as Fraunhofer lines. These lines correspond to selective absorption of the radiation at specific wavelengths due to the various elements existing in the stellar atmosphere. Stars are made up of the same elements that are found here on Earth, but in different proportions. The spectrum of a star, therefore, displays a massive number of absorption lines, which reveal a detailed fingerprint of the composition of the star. For example, over 100 000 absorption lines are visible in the Sun's spectrum.
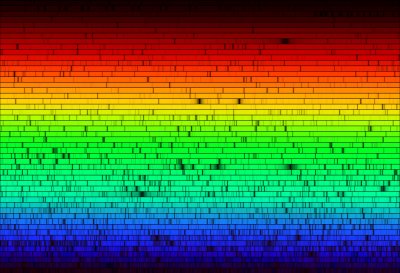 |
|
Figure 2.4: Solar Spectrum |
Spectral Classification
The ordering of stellar spectra is not immediately obvious and is a direct result of the analysis that took place around the turn of the last century.
1890 - Pickering and Fleming
Stars were sorted by decreasing hydrogen absorption-line strength. The stars were given a letter of the alphabet based on this line strength with A as the strongest and so on. Other spectral lines, such as helium, do not fit in with this sequencing.
1901 - Annie Jump Cannon
Annie Cannon was one of a number of woman working on the analysis of stellar spectra at Harvard. After studying thousands of spectra it was noticed that temperature was the principal distinguishing feature amongst different spectra and not the hydrogen line strength.
The spectral sequence was re-ordered by temperature with many classes rejected. Seven w ere left: O B A F G K M . A further ten subdivisions of each class were added by placing the numbers 0 to 9 at the end. These divisions give an indication of the presence and strength of certain elements. A useful way to remember this sequence is with the mnemonic: Oh Be A Fine Girl Kiss Me. This spectral sequence is known as the Harvard classification, although it can also be referred to as the MKK system after later development work by Morgan, Keenan and Kelman at Yerkes Observatory. Between 1911 and 1924 around 220 000 stars were analysed and published in the Henry Draper Catalog.
O type stars are the hottest with temperatures of around 40 000 K. M type stars are the coolest at around 2500 K. The Sun is an ordinary star of classification G2 and a surface temperature of around 6000 K. Hydrogen absorption lines are stongest in A type stars, as per the original classification, and lessen in both directions away from class A. The table below give the spectral classification for the ten nearest stars.
|
Star |
Name |
Class |
| Sun | G2 | |
| α CMa | Sirius | A1 |
| α Car | Canopus | A9 |
| α Cen | Rigel Ken. | G2 |
| α Boo | Arcturus | K1.5 |
| α Lyr | Vega | A0 |
| α Auriga | Capella | G6 |
| β Ori | Rigel | B8 |
| α CMi | Procyon | F5 |
| α Eri | Achernar | B3 |
| α Ori | Betelgeuse | M2 |
Table 2.1: Spectral Class of ten nearest stars
Hertzsprung-Russell Diagram
Once a star has been observed, it is useful to plot its characteristics on a chart where it can be compared with other stars. Most commonly, stars are characterised from observing their luminosity (or absolute magnitude), spectral class and/or surface temperature. These quantities are usually plotted on a Hertzsprung-Russell diagram, in which surface temperature and luminosity are set out as a logarithmic plot on an X-Y axis. The diagram is named after Ejnar Hertzsprung and Henry Norris Russell who independently developed the plot in the early 1900's.
Plotting the characteristics for a sufficient number of stars reveals groupings based on the stellar properties. The majority of stars are to be found on the Main Sequence a narrow band running across the chart from upper left to lower right. Red giants appear in the upper right of the diagram, while white dwarfs appear in the lower left quadrant. Cepheid stars appear in the middle right of the diagram in a branch extending from the Main Sequence.
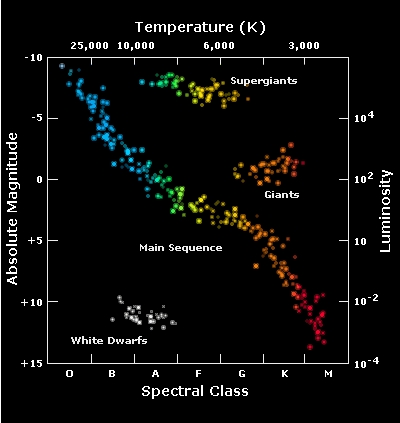 |
Figure 2.5: Hertzsprung-Russell Diagram
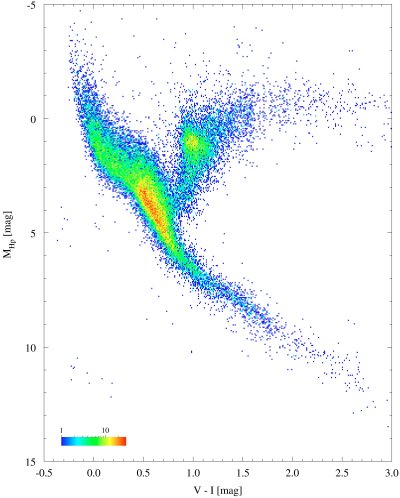 |
Figure 2.6: Actual HR Diagram Based on Hipparcos Data (ESA)
The above image is a real HR diagram generated from data on
41 453 stars in the Hipparcos catalogue. The colour scale
indicates the number of stars in a cell of 0.01 mag in V-I and
0.05 mag in MHP.
Stellar Types
For most of their lives, stars live on the Main Sequence on the HR diagram, which indicates a state of hydrostatic equilibrium and a stable structure. As the star gets older, however, it leaves the Main Sequence phase, as there is no longer sufficient hydrogen in the core to provide the correct radiation pressure to balance gravity. Once this occurs, the centre of the star contracts until it is hot enough for its helium to be converted into carbon. The outer layers of the star expand to conserve energy, making the star appear brighter and cooler. Stars at this stage are called red giants. Many of the star's outer layers are lost during this phase.
Eventually the energy being generated on the inside of such a star runs out, and it collapses to form a white dwarf.
Enormous stars with masses greater than around eight times that of the Sun, end their lives in spectacular explosions as neutron stars, which can leave behind black holes in their wake.
When they start to reach the end of their lives, stars often pulsate, producing variations in brightness, temperature and size. Cepheids (named after the star delta Cephei in the constellation of Cepheus, which can be seen with the naked eye) are stars that pulsate in a regular cycle, with rapid brightening followed by gradual dimming.
Binary Stars
Visual Binaries
Visual binary stars are those which can be seen from Earth using a telescope or binoculars. Observations of such stars dancing around each other over the course of a few nights confirm that they are binary systems.
Figure 2.6: Changing Position of a Faint Companion Star around the Bright Star Sirius
Eclipsing Binaries
Eclipsing binary stars also dance around each other, but in a distinctive way that causes one star to eclipse the other as it passes in front of it, obscuring it from the observer's sight. When the stars are next to each other, their maximum brightness can be seen by the observer, but their brightness, or magnitude, changes as the smaller star is behind or in front of the larger star.
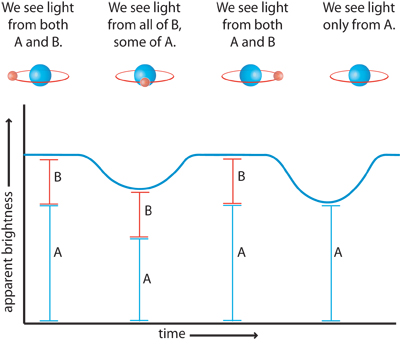 |
Figure 2.7: Simulated Lightcurve from an Eclipsing Binary
Spectroscopic Binaries
In most binaries, the stars are situated too close together for observers to distinguish them. With spectroscopic binaries it is only by analysis of stellar spectra that the binary properties are discovered.
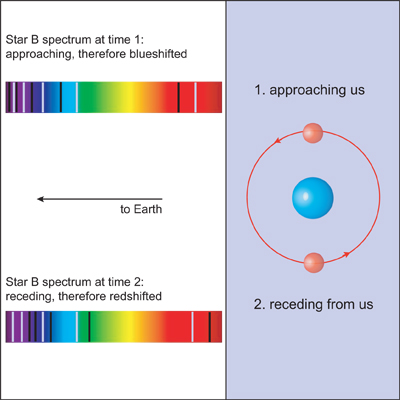 |
Figure 2.8: Spectral Shifts Observed in Spectroscopic Binary
By looking at the absorption lines in the spectrum obtained from this pair of stars, scientists can notice that as the star moves, the absorption lines also seem to move. This movement is known as the Doppler shift. Although it may be tempting to conclude that the spectrum in such a case is from a single star, as single stars are also subject to a Doppler Shift, the shift observed in the spectra of binary systems behaves in a unique way, indicating that there are two stars revolving around each other.
