ESA Science & Technology - From an almost perfect Universe to the best of both worlds

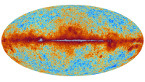
The Cosmic Microwave Background - as seen by Planck. Credit: ESA and the Planck Collaboration

It was 21 March 2013. The world's scientific press had either gathered in ESA's Paris headquarters or logged in online, along with a multitude of scientists around the globe, to witness the moment when ESA's Planck mission revealed its ‘image’ of the cosmos. This image was taken not with visible light but with microwaves.

Whereas light that our eyes can see is composed of small wavelengths – less than a thousandth of a millimetre in length – the radiation that Planck was detecting spanned longer wavelengths, from a few tenths of a millimetre to a few millimetres. Most importantly, it had been generated at very beginning of the Universe.

Collectively, this radiation is known as the cosmic microwave background, or CMB. By measuring its tiny differences across the sky, Planck's image had the ability to tell us about the age, expansion, history, and contents of the Universe. It was nothing less than the cosmic blueprint.

Astronomers knew what they were hoping to see. Two NASA missions, COBE in the early 1990s and WMAP in the following decade, had already performed an analogous set of sky surveys that resulted in similar images. But those images did not have the precision and sharpness of Planck.

The new view would show the imprint of the early Universe in painstaking detail for the first time. And everything was riding on it.

If our model of the Universe were correct, then Planck would confirm it to unprecedented levels of accuracy. If our model were wrong, Planck would send scientists back to the drawing board.
    
When the image was revealed, the data had confirmed the model. The fit to our expectations was too good to draw any other conclusion: Planck had showed us an 'almost perfect Universe'. Why almost perfect? Because a few anomalies remained, and these would be the focus of future research.

Now, five years later, the Planck consortium has made their final data release, known as the legacy data release. The message remains the same, and is even stronger.

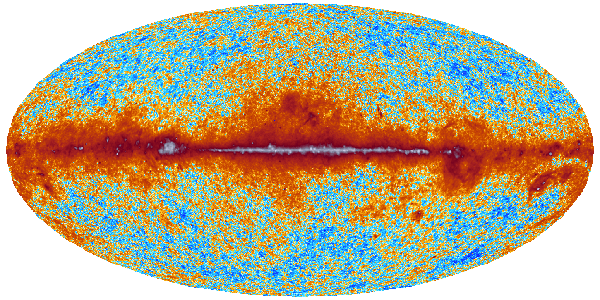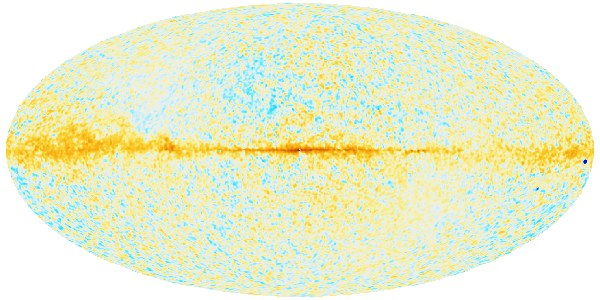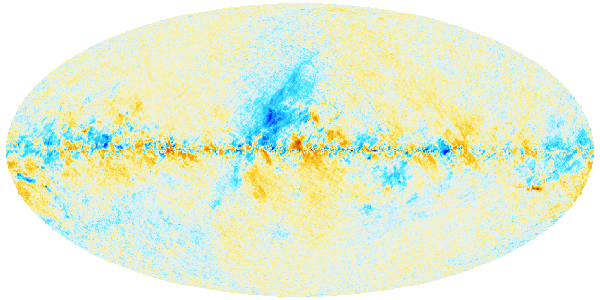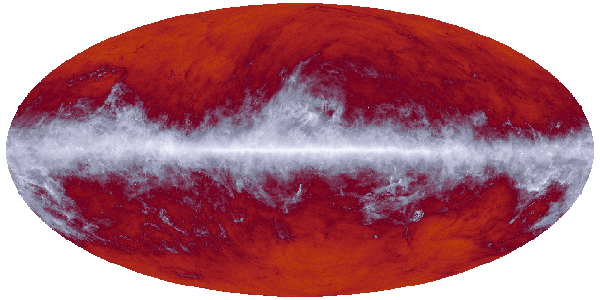Planck's view of the sky in nine channels at microwave and sub-millimetre wavelenghts. Credit: ESA and the Planck Collaboration

"This is the most important legacy of Planck," says Jan Tauber, ESA's Planck Project Scientist. "So far the standard model of cosmology has survived all the tests, and Planck has made the measurements that show it."

All cosmological models are based upon Albert Einstein's General Theory of Relativity. To reconcile the general relativistic equations with a wide range of observations, including the cosmic microwave background, the standard model of cosmology includes the action of two unknown components.

Firstly, an attractive matter component, known as cold dark matter, which unlike ordinary matter does not interact with light. Secondly, a repulsive form of energy, known as dark energy, which is driving the currently accelerated expansion of the Universe. They have been found to be essential components to explain our cosmos in addition to the ordinary matter we know about. But as yet we do not know what these exotic components actually are.

Planck was launched in 2009 and collected data until 2013. Its first release – which gave rise to the almost perfect Universe – was made in the spring of that year. It was based solely on the temperature of the cosmic microwave background radiation, and used only the first two sky surveys from the mission.

The data also provided further evidence for a very early phase of accelerated expansion, called inflation, in the first tiny fraction of a second in the Universe's history, during which the seeds of all cosmic structures were sown. Yielding a quantitative measure of the relative distribution of these primordial fluctuations, Planck provided the best confirmation ever obtained of the inflationary scenario.

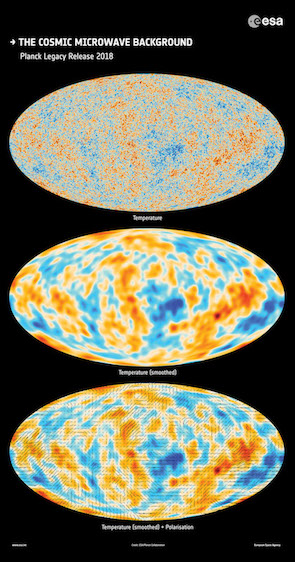Temperature and polarisation of the cosmic microwave background. Credit: ESA/Planck Collaboration

Besides mapping the temperature of the cosmic microwave background across the sky with unprecedented accuracy, Planck also measured its polarisation, which indicates if light is vibrating in a preferred direction. The polarisation of the cosmic microwave background carries an imprint of the last interaction between the radiation and matter particles in the early Universe, and as such contains additional, all-important information about the history of the cosmos. But it could also contain information about the very first instants of our Universe, and give us clues to understand its birth.

In 2015, a second data release folded together all data collected by the mission, which amounted to eight sky surveys. It gave temperature and polarisation but came with a caution.

"We felt the quality of some of the polarisation data was not good enough to be used for cosmology," says Jan. He adds that – of course – it didn't prevent them from doing cosmology with it but that some conclusions drawn at that time needed further confirmation and should therefore be treated with caution.

And that's the big change for this 2018 Legacy data release. The Planck consortium has completed a new processing of the data. Most of the early signs that called for caution have disappeared. The scientists are now certain that both temperature and polarisation are accurately determined.

"Now we really are confident that we can retrieve a cosmological model based on solely on temperature, solely on polarisation, and based on both temperature and polarisation. And they all match," says Reno Mandolesi, principal investigator of the LFI instrument on Planck at the University of Ferrara, Italy.

"Since 2015, more astrophysical data has been gathered by other experiments, and new cosmological analyses have also been performed, combining observations of the CMB at small scales with those of galaxies, clusters of galaxies, and supernovae, which most of the time improved the consistency with Planck data and the cosmological model supported by Planck," says Jean-Loup Puget, principal investigator of the HFI instrument on Planck at the Institut d'Astrophysique Spatiale in Orsay, France.

This is an impressive feat and means that cosmologists can be assured that their description of the Universe as a place containing ordinary matter, cold dark matter and dark energy, populated by structures that had been seeded during an early phase of inflationary expansion, is largely correct.

But there are some oddities that need explaining – or tensions as cosmologists call them. One in particular is related to the expansion of the Universe. The rate of this expansion is given by the so-called Hubble Constant.

To measure the Hubble constant astronomers have traditionally relied on gauging distances across the cosmos. They can only do this for the relatively local Universe by measuring the apparent brightness of certain types of nearby variable stars and exploding stars, whose actual brightness can be estimated independently. It is a well-honed technique that has been developed over the course of the last century, pioneered by Henrietta Leavitt and later applied, in the late 1920s, by Edwin Hubble and collaborators, who used variable stars in distant galaxies and other observations to reveal that the Universe was expanding.

The figure astronomers derive for the Hubble Constant using a wide variety of cutting-edge observations, including some from Hubble's namesake observatory, the NASA/ESA Hubble Space Telescope, and most recently from ESA's Gaia mission, is 73.5 km/s/Mpc, with an uncertainty of only two percent. The slightly esoteric units give the velocity of the expansion in km/s for every million parsecs (Mpc) of separation in space, where a parsec is equivalent to 3.26 light-years.

A second way to estimate the Hubble Constant is to use the cosmological model that fits the cosmic microwave background image, which represents the very young Universe, and calculate a prediction for what the Hubble Constant should be today. When applied to Planck data, this method gives a lower value of 67.4 km/s/Mpc, with a tiny uncertainty of less than a percent.

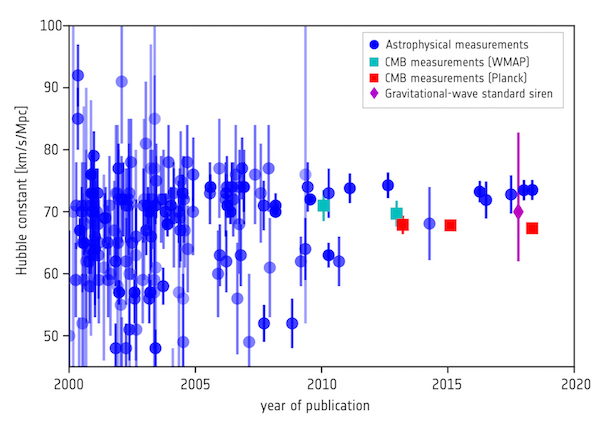Measurements of the Hubble constant over the past two decades. Credit: ESA and the Planck Collaboration

On the one hand, it is extraordinary that two such radically different ways of deriving the Hubble constant – one using the local, mature Universe, and one based on the distant, infant Universe – are so close to each other. On the other hand, in principle these two figures should agree to within their respective uncertainties. This is the tension, and the question is how can they be reconciled?

Both sides are convinced that any remaining errors in their measurement methodologies are now too small to cause the discrepancy. So could it be that there is something slightly peculiar about our local cosmic environment that makes the nearby measurement somewhat anomalous? We know for example that our Galaxy sits in a slightly under-dense region of the Universe, which could affect the local value of the Hubble constant. Unfortunately, most astronomers think that such deviations are not large enough to resolve this problem.
 
"There is no single, satisfactory astrophysical solution that can explain the discrepancy. So, perhaps there is some new physics to be found," says Marco Bersanelli, deputy principal investigator of the LFI instrument at the University of Milan, Italy.

'New physics' means that exotic particles or forces could be influencing the results. Yet, as exciting as this prospect feels, the Planck results place severe constraints on this train of thought because it fits so well with the majority of observations.

"It is very hard to add new physics alleviating the tension and still keep the standard model's precise description of everything else that already fits," says François Bouchet, deputy principal investigator of the HFI instrument at the Institut d'Astrophysique de Paris, France.

As a result, no one has been able to come up with a satisfactory explanation for the differences between the two measurements, and the question remains to be resolved.

"For the moment, we shouldn't get too excited about finding new physics: it could well be that the relatively small discrepancy can be explained by a combination of small errors and local effects. But we need to keep improving our measurements and thinking about better ways to explain it," says Jan.

This is the legacy of Planck: with its almost perfect Universe, the mission has given researchers confirmation of their models but with a few details to puzzle over. In other words: the best of both worlds.

Notes for Editors

A series of scientific papers describing the new results was published on 17 July and can be downloaded here.
The Planck Legacy Archive is available at http://pla.esac.esa.int/pla/

For further information, please contact:

Markus Bauer
ESA Science Communication Officer
Tel: +31 71 565 6799
Mob: +31 61 594 3 954
Email: markus.baueresa.int