Galactic
Water
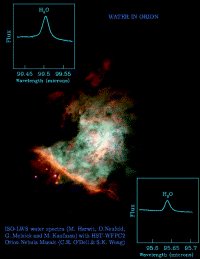
In the Orion Nebula
 |
|
Hubble image of the Orion nebula with spectra from ISO's LWS (Long Wavelength Spectrometer). |
This discovery may have also implications for the origin of water in the Solar System and on the Earth itself, and models explaining the evolution of molecular clouds where stars are born will surely have to be revised.
Planet Formation
Astronomers at the universities of Amsterdam, Louvain, Groningen and Utrecht have found proof that planets can form around old, dying stars. In the vicinity of the Red Rectangle, an old binary star in the Monoceros constellation, they have detected a ring of matter constituting the first stage of planet formation. Their results were published in Nature on 26 February 1998. It had previously been assumed that planets can form only round new-born stars.
Many young stars are ready to build planets
|
A dust disk where ISO found olivine signature. Red Rectangle imaged by ISO/MPG 2.2 microns (visible light) |
Is the Solar System a unique pearl in the Universe, the only example of planets orbiting a star? Definitely not. While other astronomers detect unseen planets by their effect on the motion of their parent stars, ISO teams see favourable circumstances for planet-making. The left-over gas and dust that swirls around many new-born stars evolves into a so-called protoplanetary disk which glows with infrared light.
Planets can form from the dust grains. When the process is over, only a thin ring of debris remains. Although no telescope has been able so far to image any alien planet, ISO has detected many of these thin debris disks, which astronomers believe are made of small bodies like comets.
Molecules
A team of astronomers from the United States and Germany discovered trace amounts of hydrogen fluoride gas in the near vacuum of interstellar space. Although approximately one hundred different kinds of molecules have been detected in interstellar space over the past 30 years, the discovery of hydrogen fluoride marks the first time that a molecule containing fluorine has been detected in an interstellar gas cloud. The discovery was reported in the Astrophysical Journal Letters. The astronomers searched for hydrogen fluoride molecules within a giant cloud of interstellar gas located near the centre of the Milky Way galaxy. The new observations were carried out with the Long Wavelength Spectrometer, one of four instruments on board ISO. Looking in the far-infrared region of the electromagnetic spectrum, the astronomers observed the telltale signature of absorption by trace amounts of hydrogen fluoride gas.
The cosmic cookery book for planets and life
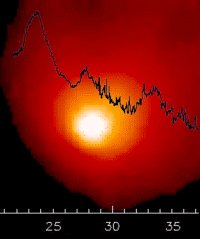 |
|
Comet Hale-Bopp and olivine signature (ESA/ISO SWS spectrum, ISOCAM image) |
ISO's ability to detect a whole variety of molecules was unprecedented and its results are now filling the blank pages of the cosmic cookery book. For instance, ISO found clear links between stars, comets and the Earth's origin. Comets are remnants of the raw materials that built the Solar System, and in the bright Comet Hale-Bopp ISO found the mineral olivine, one of the main constituents of the Earth's interior. Olivine was also detected by ISO in the dusty disks surrounding young stars, which are thought to be planetary systems in formation.
 |
|
Christoffel Waelkens |
"We are reconstructing with great detail the history of the Solar System," said Christoffel Waelkens of the University of Leuven in Belgium. "And we are linking it to other systems that are now in a critical evolutionary phase."
What about life, and the carbon chemistry on which it depends? ISO saw complex carbon-rich molecules in many places of the Universe - in interstellar space in our own Galaxy, the Milky Way, and even in other galaxies. One example is the huge bubble of organic matter that Ralf Siebenmorgen of the ISO Data Centre at Villafranca, Spain, found surrounding a young star in the Chamaeleon constellation. It is a kind of shell-like structure never detected before, made mainly of large molecules with hundreds of atoms of carbon and hydrogen. In principle these molecules could provide building blocks for living organisms.
 |
|
Carbon-rich chemicals surround a star (ESA/ISO ISOCAM R. Siebenmorgen et al.) |
Closer to home, carbon molecules found by ISO in the atmosphere of the planet Saturn included the first detection of benzene. With a simple ring-shaped molecule, benzene is best known on the Earth as a solvent, but it is the parent of a huge range of molecules used by living organisms.
The appearance of the giant planet Jupiter changes completely at different infrared wavelengths, as observed by ISO. The differences give the experts new information about the chemical composition of the atmosphere and how Jupiter's weather works.
 |
|
Jupiter at different wavelengths (ESA/ISOCAM Th. Encrenaz et al.) |
Stellar Birth
The cosmic egg from which a star will hatch
One prize sought by ISO astronomers has been the detection of the earliest stages of star formation. Pre-stellar cores are egg-like objects hidden within a larger dust cloud. A cold, thick shell of dust obscures the interior, where gas collapses under gravity to make an embryonic star. By the time the dust has dispersed, and the object inside has hatched as a plainly visible star, the main event of star formation is complete. In the earliest stages, only radio waves and far-infrared rays can escape from the dust cloud, allowing us to observe the real origins of the stars.
Derek Ward-Thompson of the Royal Observatory Edinburgh (UK) and his colleagues at Cambridge University and in France, first detected the pre-stellar core L1689B, using observations at sub-millimetre radio wavelengths, in the constellation Ophiuchus. It is a very young pre-stellar core, on the brink of collapsing to form a new star. Now the team has used ISO to make the first infrared images of L1689B using the photometer ISOPHOT at long infrared wavelengths, up to its limit of 240 microns. The shell of dust is so cold, at roughly minus 260 degrees Centigrade (or 13 K), it is undetectable even at short or medium infrared wavelengths.
Astronomers can now combine ISO's results with observations of the same object and others like it, at sub-millimetre radio wavelengths, to build up a detailed picture of the earliest stages of star formation.
A high-speed chain reaction forms new stars
Ever since a bright, massive star was born in the centre of the Trifid Nebula 100 000 years ago, it has spectacularly illuminated the dust and gas in this well-known cloud in the Sagittarius constellation. But much more has happened in the nebula in the intervening years. The energy emitted by the central star changed the physical and chemical conditions in its environment, and has provoked the quick and nearly simultaneous birth of a second generation of massive stars.
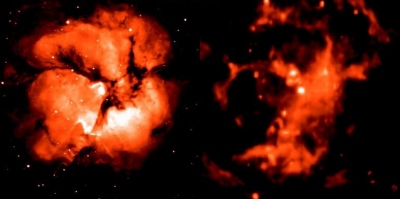 |
|
Trifid nebula by visible light (left) and by infrared light (right) (ESA/ISO ISOCAM J. Cernicharo et al.) |
 |
|
José Cernicharo |
Dying Stars
Studying a supernova
The remnant of a supernova remains discernible for thousands of years after the explosion. The most recent supernova observed in the Milky Way Galaxy occurred little more than 300 years ago and the resulting nebulous object is called Cassiopeia A. ISO has made the first detailed examination of Cassiopeia A by infrared rays unobservable from the Earth's surface. It gives direct evidence of dust formation.
Milky Way
A galactic refrigerator
The Long-Wavelength Spectrometer covered a range of the infrared spectrum entirely blotted out by the Earth's atmosphere. Instruments in high-flying aircraft and balloons have glimpsed some features in the sky at long infrared wavelengths, but only ISO offered a clear view. As a result the Long-Wavelength Spectrometer has been able to observe, in a wide variety of cosmic settings, radiation that plays an important part in cooling the Milky Way Galaxy.
Emission at a wavelength of 158 microns (about a sixth of millimetre) come from ionised carbon atoms in the clouds that fill the spaces between stars. The Long-Wavelength Spectrometer has picked up the emissions from a region where stars are being born, from a dying star, from warm and cool clouds of dust and gas, and even from extremely cold clouds of hydrocarbons called infrared cirrus. Although completely invisible to the eye, the energy shed in this way may be equivalent to the light of a billion stars. It affects the energy budget - and therefore the temperature - of the Milky Way, and of other galaxies too.
