ESA Science & Technology - Four-point observations of solar wind discontinuities

During a total eclipse of the Sun, when for a few minutes the Moon completely covers the Sun's face, a glow appears around the darkened Sun: the solar corona, the Sun's outermost atmosphere (Image 1).

Image 1: Left panel: eclipse of the Sun at solar maximum. Courtesy C.Cavadore from ESO and L. Bernasconi and B. Gaillard from Observatoire de la Cote d'Azur. Right panel: Image of the solar corona from LASCO C2 onboard SOHO.

The corona, like the Earth's atmosphere, is held down by the Sun's gravity. But the topmost layers are too hot (million degrees) to allow the Sun's gravity to hold on to the gas in these layers. Our Sun is thus continually blowing away charged particles in all directions, mainly electrons and protons. This outward flow of solar particles from the Sun is called the solar wind (Animation 1). Together with solar particles, magnetic fields are also pulled out of the Sun.

Animation 1: General presentation of the Cluster mission at solar maximum together with the SOHO mission and the ULYSSES mission.

Imagine a field line extending from the bulk of the Sun to the upper corona. The particles at its "roots" stay with the Sun, but those in the high corona flow out with the solar wind to the Earth's orbit and far beyond.

During all this time (under ideal conditions which is a fair approximation), the same field line continues to link both groups. Thus, some solar field lines will extend to the Earth and further out in the heliosphere, producing the Interplanetary Magnetic Field (IMF).

Spacecraft measurements in the interplanetary medium revealed the complexity of the solar wind flow and the IMF dynamics. In particular, large changes of the IMF direction occur twice per hour on average and last over tens of seconds. How are they created? What do they tell us about the solar corona? How do they structure the solar wind? Do they have any impact on our Earth magnetosphere?

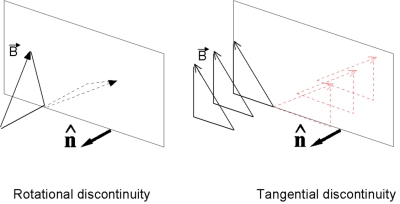
Answering all these questions is of course far beyond the scope of this webstory, however, a key step in answering some of the above questions is to determine what kind of Directional Discontinuities (DDs) are actually observed in space (Image 2). Two main types of discontinuities are usually referenced. Although observed by various spacecraft (including Ulysses and Voyager 2), the ratio between these two types remains an open question and has been so for more than 35 years.

A DD is usually classified either as tangential (TD) or rotational (RD) Magneto-Hydro-Dynamic (MHD) discontinuity. The following properties qualitatively distinguish a TD from a RD: magnitude and density changes can be significant for a TD while small for a RD; the magnetic field component, perpendicular to the plane of discontinuity, B_n, is zero for a TD while non-zero for a RD (Image 3). Therefore, the estimation of this normal is a key issue to discriminate a DD as rotational or tangential.

Before going any further, let's assume that the interplanetary medium is dominated by tangential discontinuities. This would greatly enhance our understanding of the solar wind structure. Indeed, by definition, the magnetic signature of a TD reveals the crossing of two regions magnetically not connected. In other words, when a TD is observed, the local medium is split into two distinct plasma regions, contrary to a RD. A high occurrence of TD implies that the solar wind is formed of many such regions, with no plasma flow between them. The energetic particle diffusion might also be dramatically reduced.

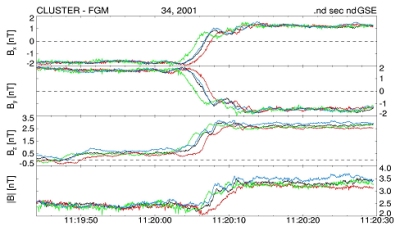
Image 2: Directional Discontinuity (DD) measured by the FGM instrument on all four Cluster spacecraft in the solar wind, free of foreshock activity.

When analysing data from a single spacecraft, the discontinuity normal is usually estimated by the Minimum Variance Analysis (MVA). The normal is identified as the direction in which the magnetic field has the least variance (minimum variance). However, no satisfying estimates of the error associated with this method exist so far.

Many of the past studies, based on single spacecraft measurements, led to the conclusion that RDs are two times more numerous than TDs [for example Neugebauer, 1984]. Two studies challenged this result by analysing multi-spacecraft observations of DDs [Burlaga and Ness, 1969; Horbury et al. 2001]. Multipoint measurements indeed allow to estimate the discontinuity normal by a more precise technique: the triangulation method, a multipoint data analysis technique. Once a discontinuity is spotted on at least three spacecraft, the relative timings between the spacecraft are used to estimate B_n (see Appendix).

Using the triangulation method, the study by Horbury et al. (2001) drew the opposite conclusion to the one found with the MVA technique: more than 2/3 of the DDs are likely to be TDs (the other study was only based on 6 cases).

At least three major issues make the validity of this conclusion questionable.

1. Only 41 DDs observed in parallel by three spacecraft have been referenced so far (35 found with GEOTAIL, WIND and IMP8; 6 found with Explorers 33, 34 and 35)
2. The triangulation method assumes that each discontinuity surface can be approximated by a plane thin sheet, over the inter-spacecraft scale. Knowing that this distance ranges from 10 R_E to 135 R_E (R_E=6378 km, the Earth's equatorial radius) for these two sets of spacecraft, the inter-spacecraft distance might not always have fulfilled this assumption. Instead, smaller distances are more likely to fulfil it
3. Using only three spacecraft, a further assumption is required: the directional discontinuity moves with the plasma bulk velocity, measured at one of the spacecraft

When four spacecraft are available, the discontinuity speed (solar wind speed plus velocity of propagation in the plasma frame) is determined by triangulation. Since its launch in 2000, the Cluster mission allows, for the first time, to analyse DDs with four spacecraft flying in close formation.

Image 3: Left panel: sketch of a rotational discontinuity where the two sides of the discontinuity are magnetically connected, as one component of the Interplanetary Magnetic Field is parallel to n, the normal of the discontinuity plane. Right panel: sketch of a tangential discontinuity which, by definition, separates two distinct plasmas, indicated by different colour of the B field arrows, both orthogonal to the normal vector.

129 DDs, observed by the four Cluster spacecraft, have been found by analysing only 22 days of magnetic field measurements in 2001 (FluxGate Magnetometer experiment, Principal Investigator: Prof. A. Balogh). The inter-spacecraft distance was around 900 km. MVA, the triangulation method and another technique were used to evaluate the RD:TD ratio.

"In agreement with single spacecraft observations, the RD:TD ratio is ~ 2 when using MVA. However, not a single proofed RD could be found with the triangulation method!", wrote Thorsten Knetter, lead author on this research, published 10 June 2004 in the Journal of Geophysical Research. Thorsten Knetter conducted this work in the Institut für Geophysik und Meteorologie, University of Cologne, Germany.

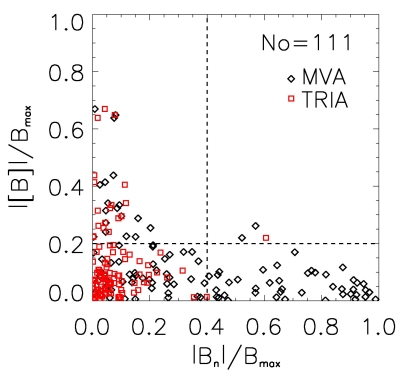
The strong discrepancy between the RD:TD ratio found with the MVA technique and the triangulation method (Image 4) has been carefully looked at and the reason found (Image 5). This investigation led to:

1. a new criterion to distinguish a RD from a TD when using MVA
2. new conditions for a safe use of MVA.

This latter result is of great interest not only for scientists working on magnetic field discontinuities. MVA is a widely spread technique among numerous scientific communities.

Contrary to Horbury et al. (2001), this study by Knetter et al. (2003) does not conclude that DDs are mostly TDs. Only 16% are classified unambiguously as TDs, when a significant change in the field magnitude occurs. "DDs could still be RDs with a small but finite B_n. Further analysis considering plasma parameters, for example, changes in velocity and density across discontinuities, has to be done", foresees Knetter.

In the near future, the analysis of Cluster measurements at all separation scales from 100 km to 5000 km, and even 10 000 km in the coming years, shall further illuminate our knowledge on the generation and the dynamics of the solar wind.  

Image 4: Scatter plot based on normal estimates from triangulation (red squares) and Cluster 4 MVA (black diamonds).

Knetter, T., F. M. Neubauer, T. Horbury and A. Balogh (2004), Four-point discontinuity observations using Cluster magnetic field data: A statistical survey, J. Geophys. Res., 109, A06102, doi:10.1029/2003JA010099

Related articles

Horbury, T. S., D. Burgess and M. Franz (2001), Three spacecraft observations of solar wind discontinuities, Geophys. Res. Lett. , 28, 677-680.

Neugebauer, M., D. R. Clay, B. E. Goldstein, B. T. Tsurutani, and R. D., Zwickl (1984), A reexamination of rotational and tangential discontinuities in the solar wind, J. Geophys. Res., 89, 5393-5408.

Russel, C. T., M. M. Mellot, E. J. Smith and J. H. King (1983), Multiple spacecraft observations of interplanetary shocks: Four spacecraft determination of shock normals, J. Geophys. Res., 88, 4739-4748.

Burlaga, L. F., and N. F. Ness (1969), Tangential discontinuities in the solar wind, Sol. Phys., 9, 467-477.

Related website
The Exploration of the Earth's Magnetosphere (David P. Stern and Mauricio Peredo) http://www.phy6.org/Education/Intro.html

Contact
Thorsten Knetter, Institut für Geophysik und Meteorologie, University of Cologne, Cologne, Germany.
Tel: +49-221-4702554

Web story author
Arnaud Masson, SCI-SH division, RSSD, ESA, The Netherlands
Tel: +31-71-565-5634

Web story editor
Philippe Escoubet, SCI-SH division RSSD, ESA, The Netherlands
Tel: +31-71-565-3454
 

Appendix

Triangulation method to estimate a magnetic discontinuity normal

Image 5: Variance ellipsoids derived from the magnetic field data for a Directional Discontinuity (DD) observed simultaneously by each Cluster spacecraft (Cluster 1,2,3 and 4 plotted respectively in black, red, green and blue)

Assuming that (1) each discontinuity surface can be approximated by a thin sheet (1D-structure) and that (2) the speed of the discontinuity is constant in time and space over the spacecraft separation distance, the orientation is simply given by R₁· n = v_nt₁ (Russell et al, 1983). Here v_n is the DD normal velocity, R₁ = (r₁₂,r₁₃,r₁₄) is a tensor with r_ij being the difference vectors of the four spacecraft positions and t₁ = (t₁₂,t₁₃,t₁₄)consists of the time differences between the corresponding spacecraft.

Using only three spacecraft Burlaga and Ness (1969) and Horbury et al. (2001) had to assume that the 1D discontinuity moves with the plasma bulk velocity measured at one of the spacecraft. The normal orientations calculated by Horbury et al. (2001) were estimated to be accurate to ~ 20^o.

If four spacecraft are available the discontinuity speed (solar wind speed plus velocity of propagation in the plasma frame) is determined by triangulation. Using the four Cluster spacecraft, the normal orientations calculated by Knetter et al. (2004) were estimated to be accurate to ~ 10^o.