O marks the spot for magnetic reconnection
10 April 2017
ESA's Cluster mission is challenging the current view of magnetic reconnection – the breaking and immediate rearrangement of magnetic field lines in the collision of two plasma flows. According to a new study, most of the energy dissipated during a reconnection event is not released at the crossings, or X-lines, between the two plasma flows but rather in swirling vortices, or O-lines, where magnetic field lines bundle up and spiral together. The new finding, which contradicts the accepted consensus, is an important step in the process of understanding the mechanisms that accelerate particles in space plasma.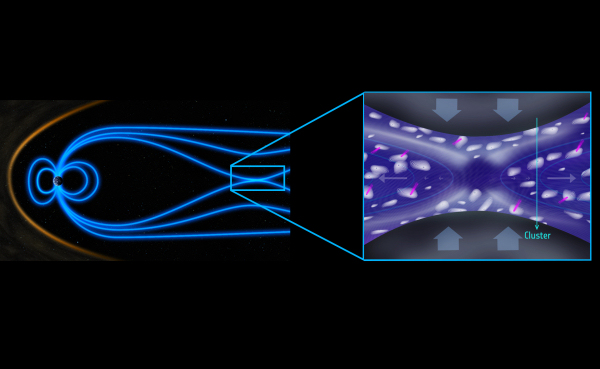 |
| X- and O-lines during magnetic reconnection in Earth's magnetosphere. Credit: ESA |
Plasma permeates the cosmos. The mixture of charged particles – electrons, protons, and heavier ions – is found in the atmosphere of the Sun, in the magnetic environment of Earth, and in the vastness of interplanetary and interstellar space.
An important phenomenon occurring in plasma is magnetic reconnection, which happens when the magnetic field lines of two colliding flows of plasma are broken and reconfigure immediately afterwards in a different geometry. In the process, the energy stored in the magnetic field is transferred to the kinetic energy of particles in the plasma, accelerating them in the form of two jets of high-speed particles launched in opposite directions.
Magnetic reconnection happens, for example, in the magnetosphere of Earth, where it is triggered by a change in the orientation of the interplanetary magnetic field carried across the Solar System by the solar wind, the stream of electrically charged particles flowing from the Sun. As a result, plasma particles are accelerated and can infiltrate the upper layer of Earth's atmosphere – the ionosphere – causing the beautiful polar lights, as well as disruptive magnetic storms that can interfere with satellites and telecommunication networks.
 |
| X- and O-lines during magnetic reconnection. Credit: ESA |
Scientists study magnetic reconnection using space missions like ESA's Cluster, which consists of four spacecraft flying in formation through the Earth's magnetic environment, as well as laboratory experiments and computer simulations.
Bridging the microscopic and macroscopic aspects of magnetic reconnection, from the particle level to the large-scale flows of matter and energy, is one of the major unsolved questions concerning this ubiquitous process. In particular, scientists are striving to understand how energy is dissipated when the magnetic field lines break, eventually leading to the acceleration of particles.
One aspect that seemed well established – the identification of the sites where energy dissipation takes place – is now being shaken up by a new study based on data from Cluster. These results call for a rethink of the standard view of magnetic reconnection.
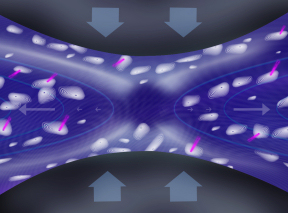 |
| X- and O-lines during magnetic reconnection (close-up view). Credit: ESA |
Under scrutiny are the two magnetic field line geometrical configurations, X-lines and O-lines, which arise when two flows of plasma collide. The main X-line is located at the crossing of the two flows, whereas smaller X-lines as well as O-lines – whirlpool-shaped vortices where the magnetic field lines swirl together – may appear throughout the broader diffusion region.
"We always thought that, in a magnetic reconnection event, energy would be dissipated at the X-lines, but the new evidence shows we've been looking at the wrong place," says Huishan Fu of Beihang University, China, lead author of the study published in Geophysical Research Letters.
"In fact, most of the energy is being dissipated at the O-lines instead."
Previous studies based on observations of magnetic reconnection events suggested that energy must be dissipated at the X-lines, which are the sites from which the two jets of high-speed particles are launched. However, these analyses did not include an accurate estimate of the location of X- and O-lines, as there was no method at that time to infer the magnetic field line geometry throughout the diffusion region.
The new study is the first to apply a recently developed method to reconstruct such topology, and it was this that enabled the scientists to reliably identify the sites of the X- and O-lines in the plasma.
The method, developed by Huishan and collaborators and published in 2015, was tested on data from Cluster and NASA's Magnetospheric Multiscale mission (MMS), which also consists of four spacecraft, as well as on the output of three-dimensional simulations. It provides the mathematical formalism not only to reconstruct the geometrical configuration of the magnetic field in the space between the four spacecraft that took the measurements, but also to expand the reconstruction to a broader region surrounding the spacecraft.
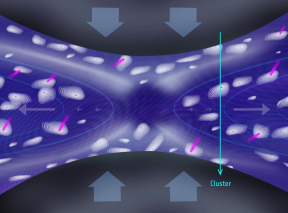 |
| Cluster's path through X- and O-lines on 9 October 2003. Credit: ESA |
The team applied this method to a magnetic reconnection event recorded by Cluster on 9 October 2003, when the spacecraft passed through a reconnection diffusion region, moving on the night side of Earth, in the magnetotail of our planet. This was a rare and valuable event because the four spacecraft were flying through the diffusion region, only about 200 km apart, where they encountered several potential sites of X- and O-lines.
"With our method, we could reconstruct the topology of the plasma that the four Cluster spacecraft had flown through," explains Huishan.
"We were extremely surprised to see that the electric current was very weak at X-lines, while it was very strong at the O-lines. This means that, contrary to our expectations, the O-lines are where most of the energy is dissipated."
The new finding, which is in stark contradiction to the present-day consensus, suggests that something profound is missing from the current understanding of magnetic reconnection.
The strong energy dissipation at O-lines is likely due to the current-driven turbulence, which is also very intense at the O-lines as revealed by Cluster. Huishan and his colleagues have not yet uncovered how exactly the current drives the small-scale turbulence; they are planning to perform a detailed analysis of this process in the future.
"This is a leap forward in our investigation of how particles are accelerated during magnetic reconnection," concludes Philippe Escoubet, Cluster Project Scientist at ESA.
"This surprising discovery shows the importance of a multi-spacecraft mission like Cluster to study space plasma."
Related publications
H. S. Fu et al. (2017), Intermittent energy dissipation by turbulent reconnection, Geophysical Research Letters, 44, 37–43, doi: 10.1002/2016GL071787
H. S. Fu et al. (2015), How to find magnetic nulls and reconstruct field topology with MMS data?, Journal of Geophysical Research: Space Physics, 120, 3758–3782, doi:10.1002/2015JA021082
For further information please contact
Huishan Fu
School of Space and Environment
Beihang University
Beijing, China
Email: hsfu![]() buaa.edu.cn
buaa.edu.cn
Phone: +86-10-82338751
C. Philippe Escoubet
Cluster Project Scientist
Directorate of Science
European Space Agency
Email: Philippe.Escoubet![]() esa.int
esa.int
Phone: +31-71-565-3454




